Cara Mudah Memahami Program Linear

Berikut merupakan langkah memahami program linear : 

1. Membuat Persamaan Garis Lurus.
a. Persamaan Umum Garis Lurus :

Contoh :

Jadi : y - 1 = 2(x - 1) = 2x - 2 sehingga didapat : y = 2x - 1 atau -2x + y = -1

b. Persamaan Garis Lurus ax + by = ab.
Contoh :

Maka persamaan garis lurusnya : 5x + 3y = 15

2. Membuat Gambar Garis Lurus.
Lazimnya dalam program linear persamaan garis dibuat dalam 2 model, diantaranya :
a. Bentuk y = mx + c
Contoh :
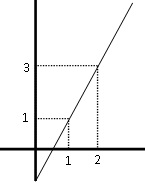
y = 2x - 1
Untuk model ini ambil sebarang nilai x.
Misal : x = 1, maka y = 2.1 - 1 = 1 didapat titik (1,1).
Misal : x = 2, maka y = 2.2 - 1 = 3 didapat titik (2,3)

b. Bentuk ax + by = c
Contoh : 5x + 3y = 15
Untuk x = 0 maka y = 2 dan didapat titik (0,5)
Untuk y = 0 maka x = 3 dan didapat titik (3,0)

3. Menentukan Wilayah
Wilayah ditentukan oleh koefisien x,sebagai berikut:
Jika koefisien x(+) dan tandanya ">=" maka wilayahnya dikanan, dan jika tandanya "<=" maka wilayahnya di sebelah kiri, sedangkan jika koefisien x(-) maka berlaku sebaliknya.

Contoh :
a. x + 2y <= 4
Koefisien x(+) dan tandanya "<=" maka wilayah sebelah kiri

b. y <= 2x + 4
Pindahkan 2x ke ruas kiri dan didapat: -2x + y <= 4
Koefisien x(-) dan tandanya "<=" maka wilayah sebelah kanan (Kebalikan dari 3.a).

5. Menentukan Titik Maksimum dan Minimum.
Menentukan titik maksimum dan minimum dibiasakan menggunakan garis selidik, dan ingat garis selidik diperoleh dari persamaan obyektifnya, caranya :
a. Lihat koefisien variabel x dan y nya.
b. Taruh koefisien x pada y begitu juga sebaliknya.
c. Hubungkan antara titik-titik perbandingan x dan y.
d. Menentukan Nilai Maksimum dan Minimum dengan aturan :
Jika koefisien x(+) maka nilai maksimum di titik yang ditemui garis selidik paling kanan, minimum kiri.
Jika koefisien x(-)  maka nilai maksimum di titik yang ditemui garis selidik paling kiri, minimum kanan.
Contoh :
Fungsi Obyektifnya : F(x,y) = 2x + 3y.

x	y
3	2
6	4
dst	dst

Contoh Soal :
Diberikan sistem pertidaksamaan :
2y >= x; y < = x; 2y + x <= 20; x + y >= 9
Berapa Nilai maksimum dari F(x,y) = 2x - y?

Jawab :
a. Pindah Ruas Variabel
Untuk memudahkan mencari wilayah dan meminimalkan hafalan maka yang dipindah ruas hanya variabel y dan buat agar nilai koefisien x positif, sehingga di dapat:
x - 2y <= 0; x - y >= 0; x + 2y <= 20; x + y >= 9

b. Buat Gambar Garis

Contoh: Ambil garis x - 2y <= 0
Untuk x = 0 maka y = 0, didapat titik (0,0)
Untuk x = 2 maka y = 1, didapat titik (2,1)

Hasil Gambar di samping.





c. Mencari Wilayah.
Contoh : Ambil garis x - 2y <= 0 karena x(+) dan tanda ">=" maka wilayah sebelah kanan.

d. Membuat Garis Selidik
Fungsi Obyektif : F(x,y) = 2x - y

x	y
-1	2
-1.-1 = 1	2.-1 = -2
dst	dst

Hasil Lengkap gambar di bawah :

Karena fungsi obyektifnya mempunya koefisien x(+), maka nilai maksimum adalah titik yang dilewati garis selidik paling kanan -> Titik yang terbentuk antara garis x + 2y = 20 dan x - 2y = 0, tinggal eliminasi keduanya dan di dapat: y = 5 dan x = 10, di dapat titik (10,5).
Jadi nilai maksimumnya : F(10,5) = 2.10 - 5 = 15

Posted in: materi